Wallis' Formula

Proposition

The following equality holds:

$$\prod _{n=1}^{\mathrm{\infty }}\frac{4n^2}{4n^2-1}=\frac{\pi }{2}$$

Alternative Forms

This expression can also be written in the following ways.

Factoring the left-hand side gives:

$$\prod _{n=1}^{\mathrm{\infty }}\frac{2n}{2n+1}\cdot \frac{2n}{2n-1}=\frac{\pi }{2}$$

Using double factorials:

$$\underset{n\to \mathrm{\infty }}{lim}\frac{(2n)!!}{(2n+1)!!}\frac{(2n)!!}{(2n-1)!!}=\frac{\pi }{2}$$

Taking the reciprocal:

$$\prod _{n=1}^{\mathrm{\infty }}(1-\frac{1}{(2n{)}^2})=\frac{2}{\pi }$$

Rewriting in terms of double factorials:

$$\underset{n\to \mathrm{\infty }}{lim}{\left(\frac{(2n)!!}{(2n+1)!!}\right)}^2(2n+1)=\frac{\pi }{2}$$

Taking the square root of both sides:

$$\underset{n\to \mathrm{\infty }}{lim}\frac{(2n)!!}{(2n+1)!!}\sqrt{2n+1}=\sqrt{\frac{\pi }{2}}$$

Multiplying both sides by $(2n)!!$:

$$\underset{n\to \mathrm{\infty }}{lim}\frac{\{(2n)!!{\}}^2}{(2n+1)!}\sqrt{2n+1}=\underset{n\to \mathrm{\infty }}{lim}\frac{\{(2n)!!{\}}^2}{\sqrt{2n+1}(2n)!}=\underset{n\to \mathrm{\infty }}{lim}\frac{(2^{n}n!{)}^2}{\sqrt{2n+1}(2n)!}=\sqrt{\frac{\pi }{2}}$$

Since $\frac{\sqrt{2n+1}}{\sqrt{2n}}\to 1$,

$$\underset{n\to \mathrm{\infty }}{lim}\frac{2^{2n}(n!{)}^2}{\sqrt{n}(2n)!}=\sqrt{\pi }$$

This form is also commonly used.

Moreover, $\frac{(2n)!}{(n!{)}^2}$ represents the number of combinations $(\genfrac{}{}{0ex}{}{2n}{n})$, so for sufficiently large $n$,

$$(\genfrac{}{}{0ex}{}{2n}{n})\sim \frac{2^{2n}}{\sqrt{n\pi }}$$

can also be interpreted as an asymptotic approximation.

Proof Using the Factorization of the Sine Function

As seen in the Basel Problem, the sine function can be formally factored as follows:

$$\sin x=x(1-\frac{x^2}{{\pi }^2})(1-\frac{x^2}{2^2{\pi }^2})\dots (1-\frac{x^2}{n^2{\pi }^2})\dots$$

Substituting $x=\frac{\pi }{2}$:

$$\sin \frac{\pi }{2}=\frac{\pi }{2}(1-\frac{(\frac{\pi }{2}{)}^2}{{\pi }^2})(1-\frac{(\frac{\pi }{2}{)}^2}{2^2{\pi }^2})\dots (1-\frac{(\frac{\pi }{2}{)}^2}{n^2{\pi }^2})\dots$$

$$1=\frac{\pi }{2}(1-\frac{1}{2^2})(1-\frac{1}{2^2{2}^2})\dots (1-\frac{1}{2^2{n}^2})\dots$$

Multiplying both sides by $\frac{2}{\pi }$:

$$\prod _{n=1}^{\mathrm{\infty }}(1-\frac{1}{(2n{)}^2})=\frac{2}{\pi }$$

Proof Using Wallis’ Integral

There is also an interesting proof using the following integral, known as Wallis’ integral:

$$I_m={\int }_0^{\frac{\pi }{2}}{\sin }^{m}xdx$$

The graph of the integrand ${\sin }^{m}x$ looks like this:

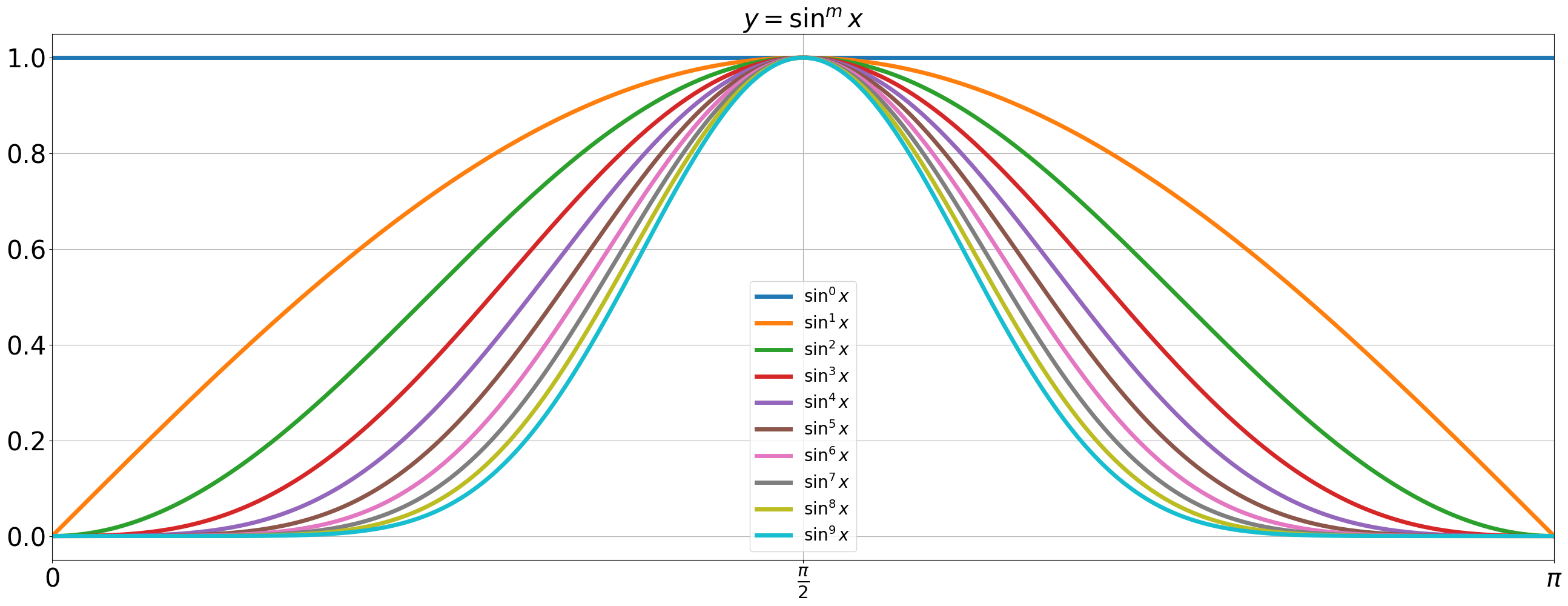
As $m$ increases, the part near $\frac{\pi }{2}$ becomes sharper, and the part near $0$ becomes gentler.

Wallis’ integral can be thought of as the area of the region enclosed by the graph of ${\sin }^{m}x$ and the $x$-axis over the interval $[0,\frac{\pi }{2}]$.

As $m$ increases, the shape of the peak becomes steeper, so the area converges to $0$.

Later, we will see that when deriving Wallis’ formula from Wallis’ integral, the ratio of $I_m$ to $I_{m+1}$ is of interest rather than the area itself.

The graph of ${\cos }^{m}x$ looks like this:

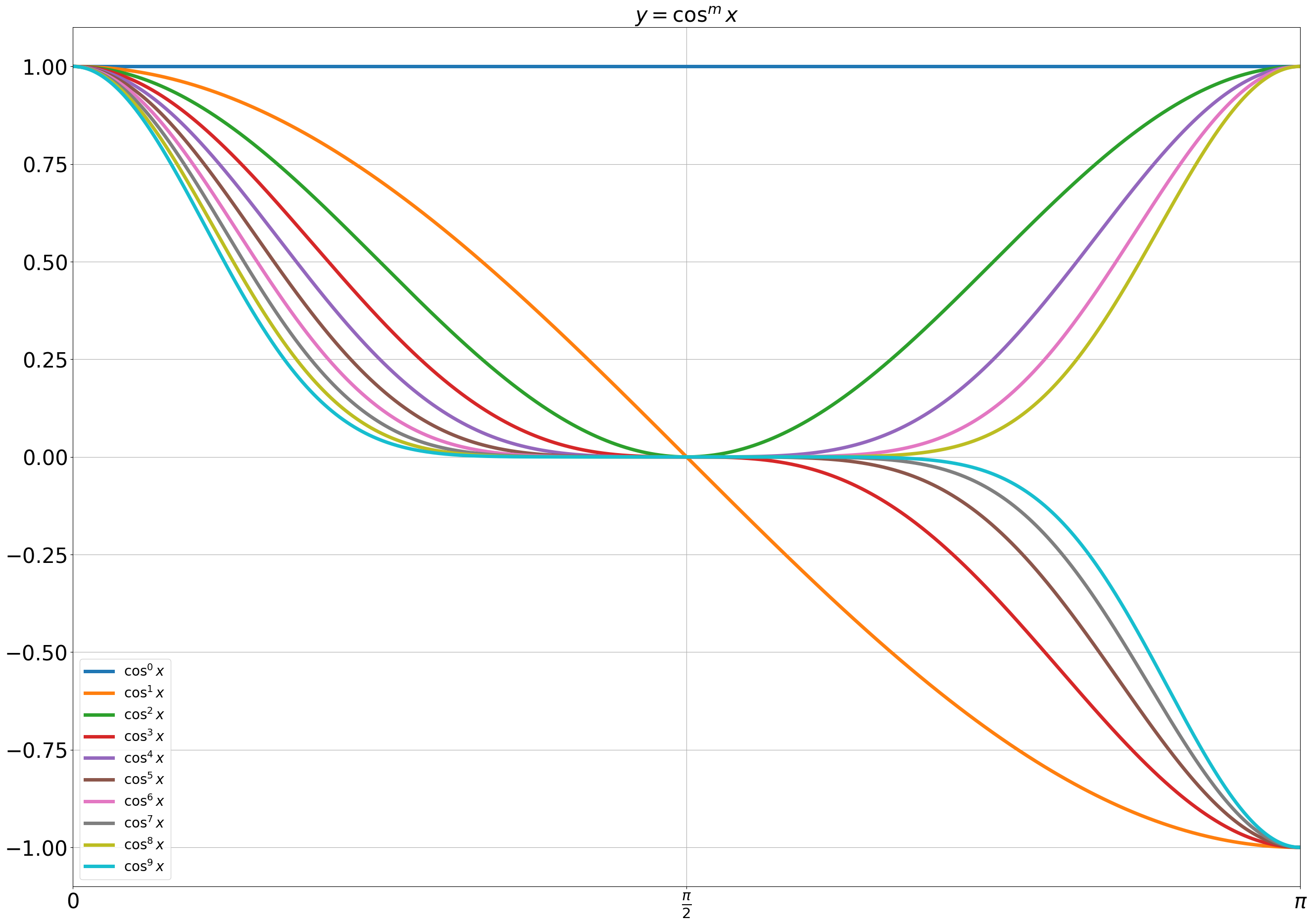
Since $[0,\frac{\pi }{2}]$ is the right half of the same peak, Wallis’ integral can also be defined as:

$$I_m={\int }_0^{\frac{\pi }{2}}{\cos }^{m}xdx$$

Now, by using integration by parts:

$$I_m={\int }_0^{\frac{\pi }{2}}{\sin }^{(m-1)}x\sin xdx$$

$$I_m=[{\sin }^{(m-1)}x(-\cos x){]}_0^{\frac{\pi }{2}}-{\int }_0^{\frac{\pi }{2}}(m-1){\sin }^{(m-2)}x\cos x(-\cos x)dx$$

$$I_m=(m-1){\int }_0^{\frac{\pi }{2}}{\sin }^{(m-2)}x{\cos }^{2}xdx$$

$$I_m=(m-1){\int }_0^{\frac{\pi }{2}}{\sin }^{(m-2)}x(1-{\sin }^{2}x)dx$$

$$I_m=(m-1){\int }_0^{\frac{\pi }{2}}{\sin }^{(m-2)}xdx-(m-1){\int }_0^{\frac{\pi }{2}}{\sin }^{m}xdx$$

$$I_m=(m-1)I_{m-2}-(m-1)I_m$$

$$m{I}_m=(m-1)I_{m-2}$$

$$I_m=\frac{m-1}{m}{I}_{m-2}$$

We obtain this recurrence relation.

Note that:

$$I_0=\frac{\pi }{2}$$

$$I_1=1$$

Applying the recurrence relation repeatedly for even and odd $m$, we get:

$$I_{2n}=\frac{(2n-1)!!}{2n!!}{I}_0=\frac{(2n-1)!!}{(2n)!!}\frac{\pi }{2}$$

$$I_{2n+1}=\frac{(2n)!!}{(2n+1)!!}{I}_1=\frac{(2n)!!}{(2n+1)!!}$$

On the other hand, since $I_m$ is a monotonically decreasing sequence,

$$0<I_{2n+1}<I_{2n}<I_{2n-1}$$

Dividing each side by $I_{2n+1}$:

$$1=\frac{I_{2n+1}}{I_{2n+1}}<\frac{I_{2n}}{I_{2n+1}}<\frac{I_{2n-1}}{I_{2n+1}}=\frac{2n+1}{2n}$$

Thus,

$$\underset{n\to \mathrm{\infty }}{lim}\frac{I_{2n+1}}{I_{2n}}=1$$

That is, the ratio of consecutive terms converges to $1$.

$$\frac{I_{2n+1}}{I_{2n}}=\frac{\frac{(2n)!!}{(2n+1)!!}}{\frac{(2n-1)!!}{(2n)!!}\frac{\pi }{2}}=\frac{2}{\pi }\frac{(2n)!!(2n)!!}{(2n+1)!!(2n-1)!!}$$

Therefore,

$$\underset{n\to \mathrm{\infty }}{lim}\frac{2}{\pi }\frac{(2n)!!(2n)!!}{(2n+1)!!(2n-1)!!}=1$$

$$\underset{n\to \mathrm{\infty }}{lim}\frac{(2n)!!(2n)!!}{(2n+1)!!(2n-1)!!}=\frac{\pi }{2}$$

Thus, Wallis’ formula is obtained.

Asymptotics of Wallis’ Integral

Now, let’s examine Wallis’ integral further. Consider the product of consecutive terms.

Using the recurrence relation:

$$I_m=\frac{m-1}{m}{I}_{m-2}$$

we have:

$$(m+1)I_{m+1}{I}_m=(m+1)\frac{m}{m+1}{I}_{m-1}{I}_m=m{I}_m{I}_{m-1}$$

Repeating this process, we get:

$$(m+1)I_{m+1}{I}_m=1I_1{I}_0=\frac{\pi }{2}$$

From the earlier result, $I_{m+1}\sim I_m$, and since $m+1\sim m$, we have $m{I}_m^2\sim \frac{\pi }{2}$.

That is,

$$\underset{m\to \mathrm{\infty }}{lim}\sqrt{m}{I}_m=\sqrt{\frac{\pi }{2}}$$

and

$$I_m\sim \sqrt{\frac{\pi }{2m}}$$

This can be seen by graphing Wallis’ integrals:

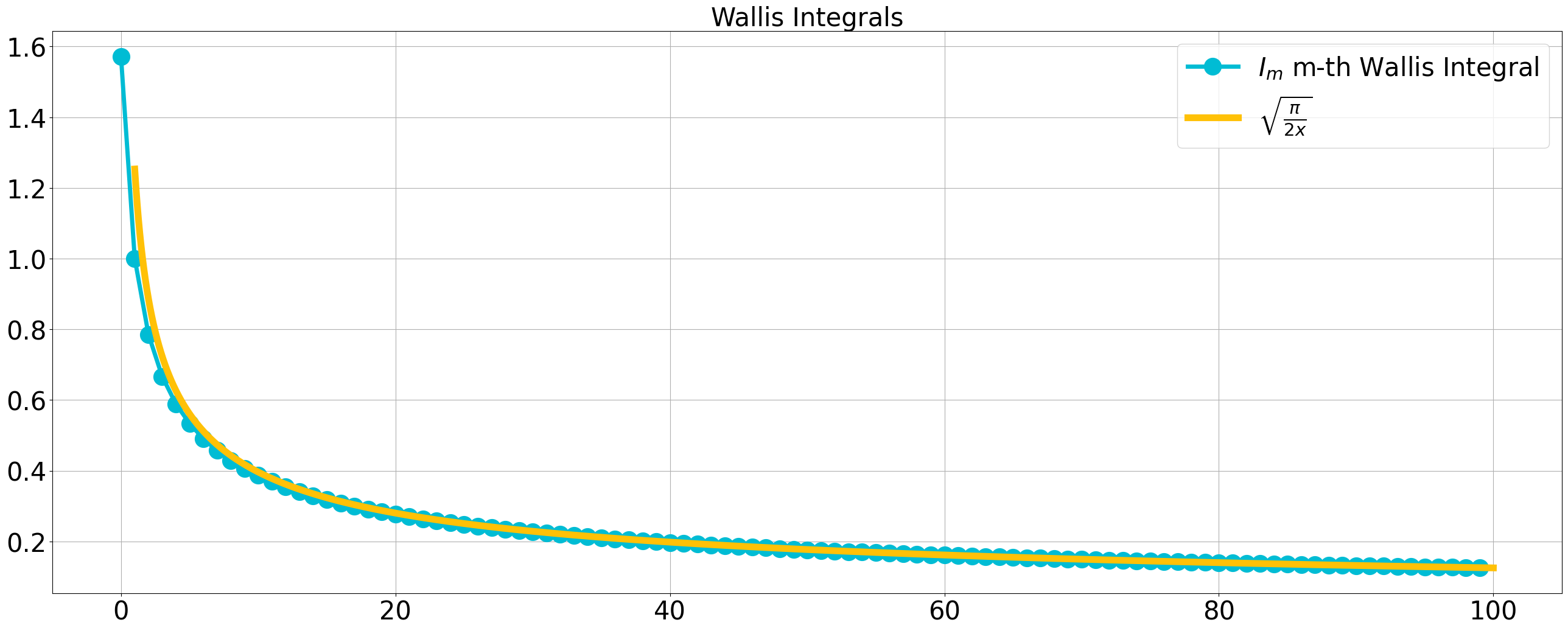
Additional Notes

Wallis’ formula implies that the coefficient of $x^n$ in $(1+x{)}^{2n}$ is approximately $4^n/\sqrt{n\pi }$.

It is sometimes used in the proof of Stirling’s formula, which approximates factorials (or the gamma function).

It is also used to compute the Gaussian integral and has various other applications.