Proof of the Gaussian Integral Using the Wallis Integral

Proposition

The following holds:

$$ \int_{-\infty}^{\infty}e^{-x^2}dx = \sqrt{\pi} $$

Proof

Lemma

For $x \ne 0$, the following inequalities hold:

$$ 1 - x^2 < e^{-x^2} < \frac{1}{1 + x^2} $$

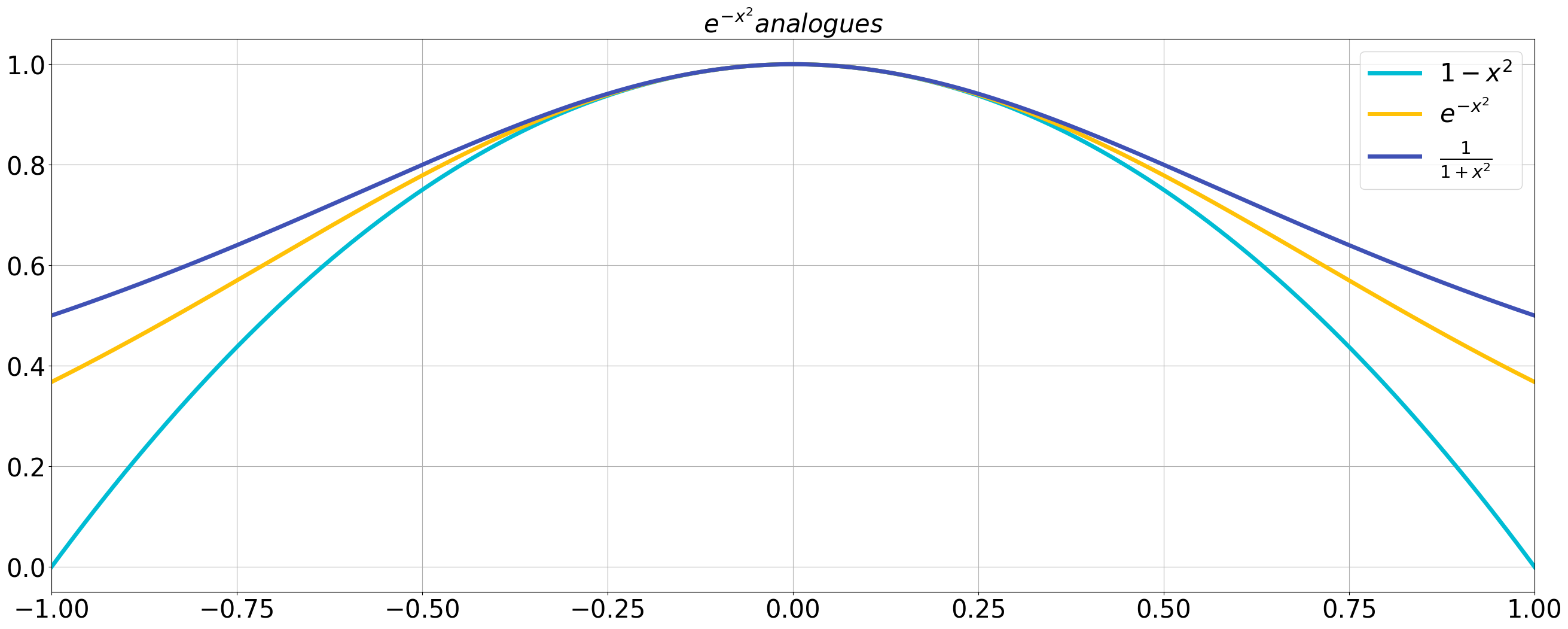
Proof of the lemma

For $x \ne 0$,

$$ e^x > 1 + x $$

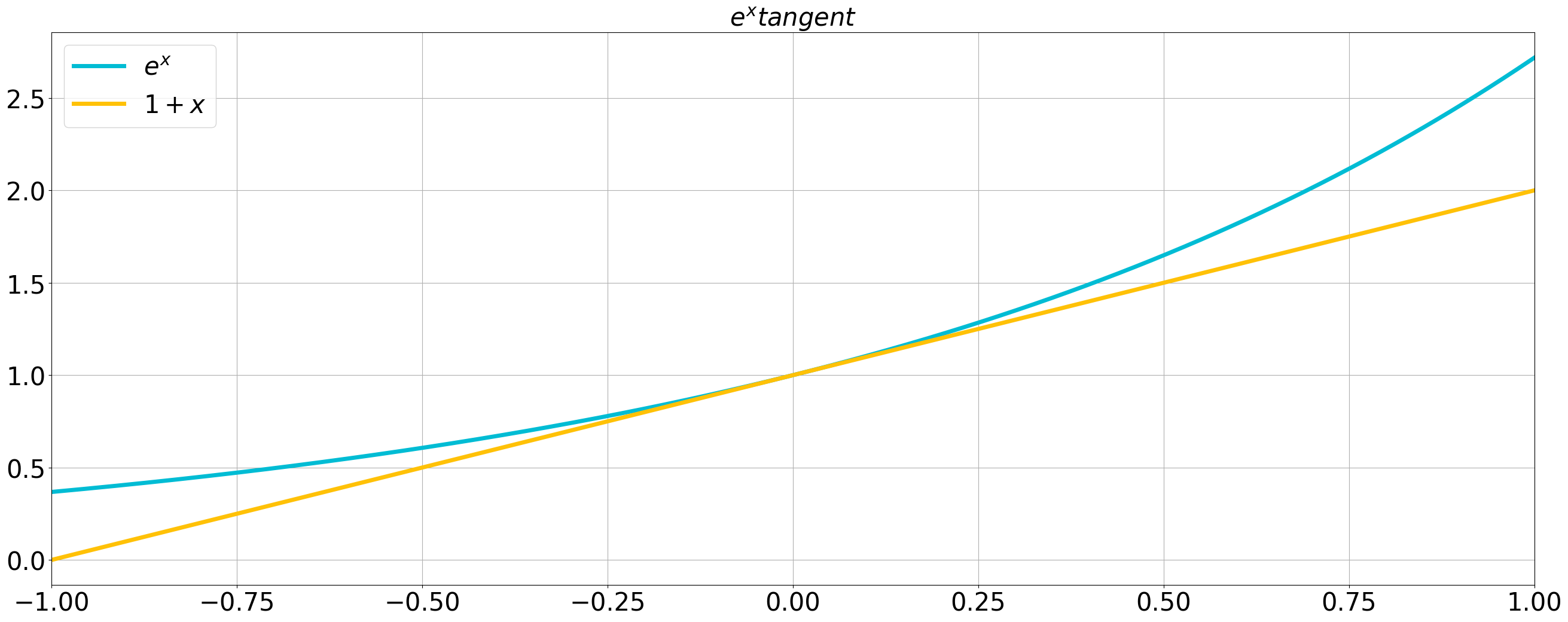
In fact, the right-hand side is the Taylor expansion truncated after the second term of the left-hand side, representing the tangent line of $y = e^x$ at $x=0$.

Since $y = e^x$ is convex (as $e^x > 0$ even after two derivatives), $y = e^x$ lies above the tangent line $y = 1 + x$.

Therefore, $ e^x > 1 + x $ holds.

By substituting $-x^2$ for $x$ in this inequality, we get $1 - x^2 < e^{-x^2}$.

Also, substituting $x^2$ for $x$ and taking the reciprocal gives $e^{-x^2} < \frac{1}{1 + x^2}$.

Substitution in the Wallis Integral

Consider the Wallis integral

$$ I_m = \int_{0}^{\frac{\pi}{2}}{\sin^m{x}dx} $$

Substitution $y=\cos{x}$

By subsituting $y=\cos{x}$ for $I_{2n+1}$,

$$ I_{2n+1} = \int_{0}^{\frac{\pi}{2}}{\sin^{2n}{x}\sin{x}dx} = \int_{1}^{0}{(1 - y^2)^n(-\frac{dy}{dx})dx} = \int_{0}^{1}{(1 - y^2)^ndy} = \int_{0}^{1}{(1 - x^2)^ndx} $$

Substitution $y=\cot{x}$

By subsituting $y=\cot{x}$ for $I_{2n+1}$,

$$ I_{2n-2} = \int_{0}^{\frac{\pi}{2}}{\sin^{2n}{x}\frac{1}{\sin^2{x}}dx} = \int_{\infty}^{0}{\frac{1}{(1 + y^2)^n}(-\frac{dy}{dx})dx} = \int_{0}^{\infty}{\frac{1}{(1 + y^2)^n}dy} = \int_{0}^{\infty}{\frac{1}{(1 + x^2)^n}dx} $$

Evaluation of the Gaussian Integral

Let

$$ I = \int_{0}^{\infty}e^{-x^2}dx $$

By substituting $x = \sqrt{n}y$,

$$ I = \int_{0}^{\infty}e^{-ny^2} \sqrt{n}dy = \sqrt{n}\int_{0}^{\infty}e^{-nx^2} dx $$

From the lemma,

$$ \sqrt{n}\int_{0}^{1}(1-x^2)^n dx < \sqrt{n}\int_{0}^{1}e^{-nx^2} dx < I < \sqrt{n} \int_{0}^{\infty}\frac{dx}{(1+x^2)^n} $$

Since the leftmost and rightmost terms are in the same form as the Wallis integral after substitution, we ultimately have:

$$ \sqrt{n}I_{2n+1} < I < \sqrt{n}I_{2n-2} $$

As seen from Wallis' Formula,

$$ \lim_{m \to \infty} \sqrt{m}I_{m} = \sqrt{\frac{\pi}{2}} $$

so,

$$ \sqrt{n}I_{2n+1} = \frac{\sqrt{n}}{\sqrt{2n+1}}\sqrt{2n+1}I_{2n+1} \to \frac{1}{\sqrt{2}} \sqrt{\frac{\pi}{2}} = \frac{\sqrt{\pi}}{2} (n \to \infty) $$

$$ \sqrt{n}I_{2n-2} = \frac{\sqrt{n}}{\sqrt{2n-2}}\sqrt{2n-2}I_{2n-2} \to \frac{1}{\sqrt{2}} \sqrt{\frac{\pi}{2}} = \frac{\sqrt{\pi}}{2} (n \to \infty) $$

Therefore,

$$ I = \frac{\sqrt{\pi}}{2} $$

Adjustment of the Integration Interval

Since the integrand is an even function,

$$ \int_{-\infty}^{\infty}e^{-x^2}dx = 2I = \sqrt{\pi} $$

Thus, the result is proved.